基础数学¶
一、微积分¶
-
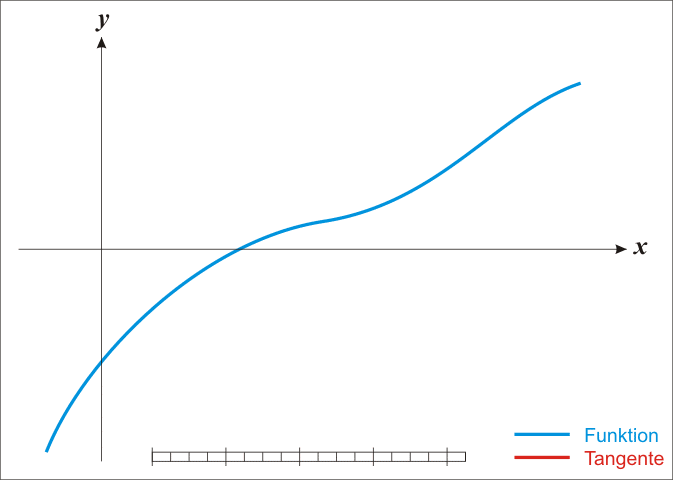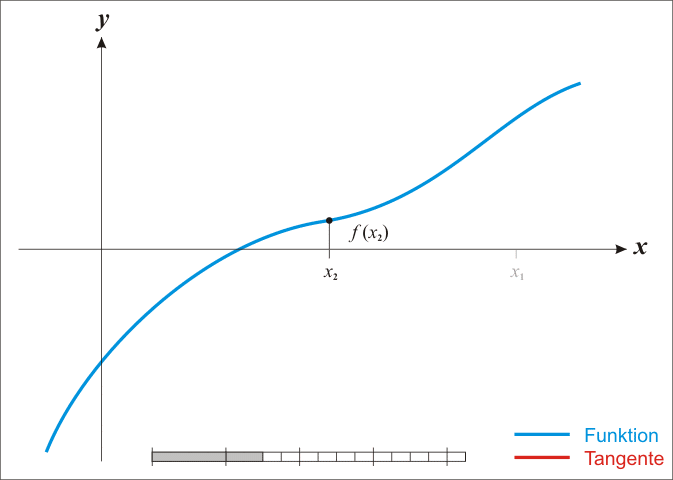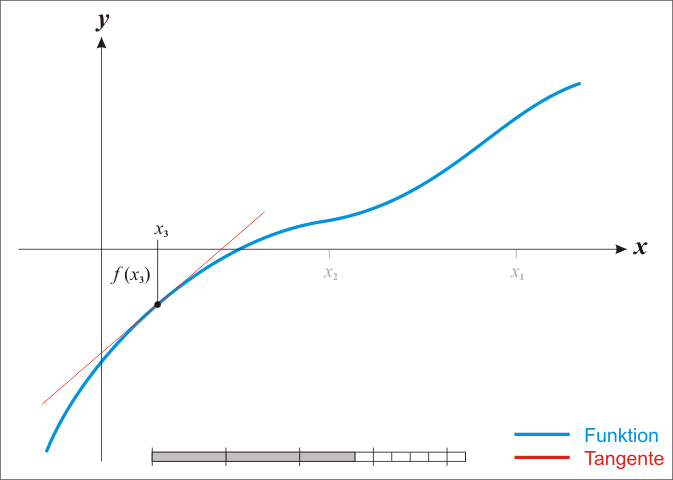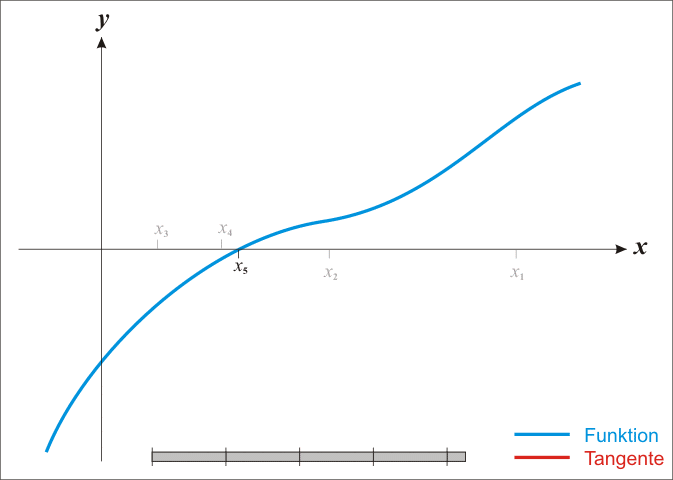
导数¶
定义: 导函数值,微商。
记作: \(f^‘(x_0) 或 \frac{df(x_0)}{dx} 或 \frac{dy}{dx}\)
作用:求极值
-
左右导数与可导函数¶
-
神经网络激活函数¶
- Sigmoid激活函数
\(\sigma = \frac{1}{1+e^{-x}}\)
- Tanh激活函数
\(tanh(x) = 2\sigma(2x)-1\)
- Softmax 激活函数
Softmax 函数将多个标量映射为一个概率分布
\(y_i=softmax(z_i)=\frac{e^{z_i}}{\sum_{j=1}^Ce^{zj}}\)
\(y_i\)表示第i个输出值,即属于类别i的概率 \(\sum_{j=1}^Cy_i=1\)
\(z=W^tx\) 表示线性方程,Softmax函数用于多分类
-
泰勒函数¶
函数f(x) 在\(x_o\)的某个开区间(a,b)上具有(n+1)阶导数,那么对于任意 \(x\in(a,b)\)
某一点的各阶导数值做系数,构建一个多项式来近似表达这个函数
- 一阶泰勒公式
\(f(x+∆x)\approx \frac{f(x)}{0!} + \frac{f^‘(x)}{1!}∆x\)
- 二阶泰勒公式
\(f(x+∆x)\approx \frac{f(x)}{0!} + \frac{f^‘(x)}{1!}∆x + \frac{f^{‘‘}(x)}{2!}∆x^2\)
二、线性代数¶
-
向量运算法则¶
-
λ(μA) = λμ(A)
- (λ +μ)A = λ A + μA , λ(A+B) = λA + λB
- AB = BA
- (A+B)C = AC+BC
-
(λA).B = λ(AB)
-
向量范数¶
范数的公式是向量每个分量绝对值的P次方,在用幂函数计算P分之一,P是整数 1,2,3,。。。∞
向量的范数就是把向量变成一个标量, 范数的表示就是两个竖线表示,让后右下角写上P
-
范数(曼哈顿距离) \(\lVert A \lVert_1=\sum_{i=1}^n\lvert x_i\lvert\)
向量元素绝对值之和 表示X到零点的曼哈顿距离
-
2范数(欧式距离) \(\lVert A \lVert_2= \sqrt{\sum_{i=1}^n x_i^2}\)
向量元素的平方在开方,欧几里得范数 ,常计算向量长度,表示X到零点的欧式距离
-
P范数 \(\lVert A \lVert_P=\left[ \sum_{i=1}^n\lvert x_i\lvert ^p\right]^{\frac{1}{p}}\)
向量元素绝对值的P次方和\({\frac{1}{p}}\)次幂,表示X到零点的P阶闵氏距离
-
∞范数 \(\lVert A \lVert _∞=max_i\lvert x_i \lvert\)
当P趋向于正无穷时,所有向量元素绝对值中的最大值,表示切比雪夫距离
-
特殊向量¶
-
0向量
[0,0,0,0,0]
-
单位向量
2范数为1 模为1,长度为1的向量
向量 \(\overrightarrow{AB}\)的长度叫做向量的模,记作 \(\lvert\overrightarrow{AB}\lvert\)
计算公式:(x,y) 模长 \(\sqrt{x^2+y^2}\)
-
常见矩阵¶
-
方阵 m=n
\(A=\begin{bmatrix} 1 & 2 & 3 \\ 3 & 4 &5 \\ 3 & 4 &5 \\ \end{bmatrix}\)
-
对称矩阵 \(a_{ij}=a_{ji}\)
\(A=\begin{bmatrix} 1 & 2 & 3 \\ 2 & 4 &5 \\ 3 & 5 &7 \\ \end{bmatrix}\)
-
单位矩阵 对角线都是1,其他位置是0,单位矩阵写作为\(I\)等同于数字1
\(A= \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 &0 \\ 0 & 0 &1 \\ \end{bmatrix}\)
-
对角矩阵,主对角线非0,其他位置是0
\(A= \begin{bmatrix} λ_1 & 0 & 0 \\ 0 & λ_2 &0 \\ 0 & 0 & λ_3 \\ \end{bmatrix}\)
-
矩阵的运算法则¶
-
A+B+C = (A+B)+C
- (AB)C = A(BC)
- (A+B)C = AC+BC
- AB ≠ BA
-
\((AB)^T=A^TB^T\)
-
逆矩阵¶
-
定义
\(AB=I 或者 BA=I\)
\(A=B^{-1}\)
\(B=A^{-1}\)
A的逆矩阵 \(A^{-1}\)
\(AA^{-1}=I=1\)
-
作用及公式
\(XW=Y\) \(X^{-1}XW=X^{-1}Y\)
\(IW=X^{-1}Y\)
\(W=X^{-1}Y\)
-
行列式¶
行列式把矩阵变成一个标量
\(\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{bmatrix} =a_{11}a_{22}-a_{12}a_{21}\)
\(\begin{bmatrix} a_{11} & a_{12}& a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{bmatrix}\) \(=a_{11}a_{22}a_{33}+a_{12}a_{22}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{11}a_{23}a_{32}\)
-
伴随矩阵¶
-
代数余子式 \(A_{ij}=(-1)^{i+j}M_{ij}\)
\(A= \begin{bmatrix} a_{11} & a_{12}& a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{bmatrix}\)
\(A_{33}= \begin{bmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{bmatrix}\)
-
伴随矩阵
\(A= \begin{bmatrix} a_{11} & a_{12}& a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{bmatrix}\)
\(A^*= \begin{bmatrix} A_{11} & A_{21}& a_{31} \\ A_{12} & A_{22} & A_{32} \\ A_{13} & A_{23} & A_{33} \\ \end{bmatrix}\)
代数余子式的行列式:
\(A_{11}=a_{22}a_{33}-a_{23}a_{32}\)
-
伴随矩阵的性质
\(AA^*=A^*A=|A|I\)
-
公式
\(AA^*=|A|AA^{-1}\)
\(A^*=|A|A^{-1}\)
\(A^{-1}=\frac{A^*}{\lvert A\lvert}\)
-
特征值与特征向量¶
-
定义:A是你阶方阵,如果存在数λ和非零年为列向量µ,使的\(A \overrightarrow{v} = λ\overrightarrow{v}\)成立,则称λ式矩阵A的一个特征值,\(\overrightarrow{v}\)是特征值λ的特征向量
实对称矩阵特征值为实数,非对称举止和复矩阵特征值可能为复数
-
满秩矩阵:
A是n阶矩阵,若r(A)= n 则称A为满秩矩阵,但满秩矩阵不限于n阶矩阵,若矩阵等于行数,称为行满秩。若矩阵等于列数,称为列满秩。既是行满秩又是列满秩则为n阶矩阵及n阶方阵
-
示例
所有的特征值的乘积等于A的行列式
\(\prod_{i=1}^nλ_i=\lvert A\lvert\)
-
特征值分解
特征值分解,就是将矩阵A分解为如下式:
\(A=Q\sum Q^{-1}\)
其中,Q是矩阵A的特征向量组成的矩阵,\(\sum\)则是对角阵,对角线上的元素就是特征值。
\(\sum= \begin{bmatrix} λ_1 & & \\ & λ_2 & \\ & & λ_n \\ \end{bmatrix}\)
对称矩阵那么Q是正交矩阵(列和行相等),正交矩阵的定义Q的逆等于Q的转置
\(Q^{-1}=Q^T\)
意义:特征值的大小表示这个特征到底有多重要,提取这个矩阵最重要的的特征
-
矩阵的向量的求导公式¶
-
奇异值分解(SVD)¶